Archive for October, 2010

Building a Retrosheet Database, Part 1

Wednesday, October 27th, 2010

I want to be able to calculate Tangotiger’s WPA/LI stat (Win Probability Added/Leverage Index, a.k.a. situational wins, context neutral wins, or game state linear weights). To do that, I need to be able to calculate WPA and LI. To do that, I need to construct a Win Expectancy matrix. To do that, I need to build a Retrosheet database. So that’s where I’m going to start. I’ve never worked with a database or explored any Retrosheet data before, so I am starting from scratch (though I will be utilizing a lot of great resources from around the web). In a series of posts I will describe my process step-by-step. If you want to follow along, make sure you have a lot of free disk space (the parsed data files for all seasons take up over 5 GB). Also be aware that some of my instructions will be Windows-specific.

(more…)

Posted in Databases, Retrosheet, Run/Win Expectancy | 2 Comments »

The Distribution of Talent Between Teams

Wednesday, October 20th, 2010

Four years ago Tango had a very interesting post on how talent is distributed between teams in different sports leagues. I want to revisit and expand upon some of the points that came up in that discussion.

First, lets look at some empirical data. I scraped end of season records from the last ten years for the NFL, NBA and MLB from ShrpSports (I decided to omit the NHL from this analysis due to the prevalence of ties). The data is available here (click through) as a tab-delimited text file. I used R to analyze the data. If you don’t have R you can download it for free (if you use Windows I recommend using it in conjunction with Tinn-R, which is great for editing and interactively running R scripts). Here is the R code I used:

?View Code RSPLUS 
records = read.delim(file = "records.txt")
lgs = data.frame(league=c("NFL","NBA","MLB"),teams=c(32,30,30),games=c(16,82,162))
lgs$var.obs[lgs$league == "NFL"] = var(records$win_pct[records$league == "NFL"])
lgs$var.obs[lgs$league == "NBA"] = var(records$win_pct[records$league == "NBA"])
lgs$var.obs[lgs$league == "MLB"] = var(records$win_pct[records$league == "MLB"])
lgs$var.rand.est = .5*(1-.5)/lgs$games
lgs$var.true.est = lgs$var.obs - lgs$var.rand.est
lgs$regress.halfway.games = lgs$games*lgs$var.rand.est/lgs$var.true.est
lgs$regress.halfway.pct.season = lgs$regress.halfway.games/lgs$games
lgs$noll.scully = sqrt(lgs$var.obs)/sqrt(lgs$var.rand.est)
lgs$better.team.better.record.pct = 0.5 + atan(sqrt(lgs$var.obs - lgs$var.rand.est)/sqrt(lgs$var.rand.est))/pi
lgs

Here is the resulting table:

(more…)

Posted in Comparing Sports, R, Simulation, Talent Distribution | 7 Comments »

The Origins of Log5

Sunday, October 3rd, 2010

Of all Bill James’ sabermetric innovations, my favorite has always been the log5 formula for determining matchup probabilities. It provides a method for taking the strengths of two teams and estimating the probability of one team beating the other. It can also be applied to individual player matchups, such as a batter facing a pitcher.

Here is a common way to express the formula for the context of team matchups:

Win\%_{A vs. B} = \dfrac{Win\%_A \times (1 - Win\%_B)}{(Win\%_A \times (1 - Win\%_B)) + ((1 - Win\%_A) \times Win\%_B)}

Unfortunately this formulation doesn’t shed much light on why James called this log5, or where the formula came from in the first place.

James’ Original Formulation

James introduced the formula in the 1981 Baseball Abstract, which is excerpted here. In his initial presentation, James first converted each team’s winning percentage (or 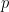p, their probability of success) into what he called their log5.

\dfrac{log5}{log5 + .500} = p

Solving for log5:

log5 = .500 \times \dfrac{p}{1 - p}

After this conversion, the formula is simple:

p_{AvB} = \dfrac{log5_A}{log5_A + log5_B}

Logarithms, Odds, and Odds Ratios

So where does the “log” in log5 come from? I’m not sure exactly where James got it, but there is a connection to the logit function:

logit(p) = log\left(\dfrac{p}{1 - p}\right)

That  \frac{p}{1 - p} term was present in James’ formulation. It is what is known as the odds. It’s common term in gambling — if some event has a .75 probability, the odds are \frac{.75}{(1 - .75)} = 3, typically expressed as 3:1 or 3 to 1.

Framing things in terms of odds rather than probabilities can be helpful.

Odds = \dfrac{p}{1 - p}

We can replicate the log5 formula by simply taking the odds ratio, which is just the odds for team A divided by the odds for team B.

OddsRatio_{AvB} = \dfrac{Odds_A}{Odds_B}

To convert this back to a probability we need one final step:

p_{AvB} = \dfrac{OddsRatio_{AvB}}{1 + OddsRatio_{AvB}}

Combining these steps, we have a simple formulation of log5:

p_{AvB} = \dfrac{Odds_A}{Odds_A + Odds_B}

This matches James’ original formulation, but here we see that one can use simple odds rather than James’ log5 term (which contains an unnecessary .500 multiplier).

Tying this back into the logit function, we can reformulate log5 to say that the matchup probability is equal to the inverse-logit of the log of the odds ratio (of course, it’d be simpler to just say that the matchup odds are equal to the odds ratio, but then we’d be leaving the “log” out of “log5″).

The “5″ in “log5″ and a More General Formulation

The “5″ part of “log5″ was in reference to the fact that teams were being compared to .500, the average winning percentage. But when we’re dealing with individual matchups, the league average isn’t always .500 (for a batter/pitcher matchup to estimate the probability of a hit, we would need to use the league-wide batting average). To deal with this we need to add another term to the formula representing the league average probability (or odds).

In the odds ratio formulation, this is easy. We just divide by the league average odds (Odds_{LG}). When the league average probability is .500, the odds are \frac{.500}{(1 - .500)} = 1, so the term can be omitted without consequence.

OddsRatio_{AvB} = \dfrac{\frac{Odds_A}{Odds_B}}{Odds_{LG}}

Converting this to a probability, we have what I find to be the clearest formulation of the generalized log5 formula:

p_{AvB} = \dfrac{Odds_A}{Odds_A + (Odds_B \times Odds_{LG})}

Precedents

So was Bill James the first to discover the log5 formula? Not exactly. It turns out that log5 is a variation of the Bradley-Terry model for pairwise comparison, which was first published in 1952 (and which itself was a variation on a 1929 work of German mathematician Ernst Zermelo). The formula given on the Wikipedia page is equivalent to the inverse-logit formulation I discussed above, if the logs of each team’s odds are used for the scale locations (their formula uses the difference of the logs of the odds, which is equal to the log of the ratio of the odds that I used). Jim Albert and Jay Bennett discussed the Bradley-Terry model in of their excellent book, “Curve Ball.” The Bradley-Terry model has been used for rating systems in many sports, including hockey and chess (I highly recommend Mark Glickman’s article “A Comprehensive Guide to Chess Ratings” for more background on paired comparisons and the connection between log5/Bradley-Terry and the logistic distribution).

For more on log5, here’s a good early piece by Dean Oliver, which includes a shortcut formula that mirrors one discussed by Joe Arthur in a great thread from Tango’s blog. Mike Tamada has also written some lucid intros to log5 and . Hal Stern’s work on paired comparisons is worth hunting down – he explicitly makes the link between the logit function and log5 in of “Statistical Thinking in Sports” (for more references to his work see this comprehensive bibliography on sports ranking systems, which points to a lot of other relevant articles). Padres analyst Chris Long also made the connection between log5 and Bradley-Terry in a presentation he gave last year. And finally, Steven Miller has written a nice short paper that provides a justification of log5 using the geometric series formula.

Posted in Log5 | 1 Comment »